Doctsf (Modèles & Marques)
AnnoncesJe suis certain que j’avais noté quelque part la véritable formule pour calculer la longuer exacte d’une courroie.
La formule des deux demi circonférences + deux fois l’entraxe ça ne peut pas marcher !
Le bout de ficelle qu’on mesure après c’est bien, mais je cherche la vraie formule !
C’est à dire:
Dia. 1 = XXX
Dia. 2 = XXX
Entraxe = XXX
Quelqu’un s’en souvient ?
Merci d’avance
Daniel
Sur google, en tapant « longueur courroie » il y a plusieurs solutions.
Merci Pierre
Amitiés
Daniel
Si Daniel, deux-fois l’entr’axe plus deux demi-circonférences (donc une circonférence entière 
si les deux poulies ont le même diamètre), cela donne bien la longueur de l’intérieur de la courroie si l’on a pris pour le calcul le diamètre de la gorge de la poulie (ou des poulies en cas de diamètres différents.
Pour avoir la longueur de la courroie, il faut tenir compte de son épaisseur qui augmente d’autant le diamètre des poulies.
Conclusion, le diamètre à prendre en compte pour chaque demi-circonférence est égal au diamètre de la gorge de la poulie augmenté d’une demi-épaisseur de courroie (c’est à dire d’un demi-diamètre de courroie si c’est une courroie de section ronde).
Bon calcul 
Merci
Mais il s’agit de deux poulies de dia 204 et 6mm entraxe 118 mm donc le calcul des demi circoférences ne s’applique pas dans ce cas !
Amitiés
Daniel
Voici la formule magique que j’ai établie par la géométrie pour des poulies de rayons différents sur tableur de works.
=2RACINE(D^2-(Rb-Ra)^2)+PI()(Ra+Rb)+2ASIN((Rb-Ra)/D)(Rb-Ra)
D: Distance entre les centres des poulies
Ra: rayon d’une poulie
Rb: rayon de l’autre poulie.
J’espère qu’elle est correcte.
PS: je n’arrive pas à joindre le fichier du tableur correspondant sur le forum!!!
Ra 102
Rb 3
D 118
L 655,3799214
NB: pour un calcul précis, il faudrait ajouter la demi-épausseur de la courroie à chacun des rayons.
Merci beaucoup M. Greuet
C’est exactement ce que je cherchais.
De toute façon, l’épaisseur de la courroie n’a pas une très grande importance, il faut diminuer la longueur théorique pour obtenir une certaine tension pour éviter que la courroie ne patine.
Et ça c’est vraiment au pif ( et en fonction des tailles disponibles )
Je garde précieusement votre formule.
Amitiés
Daniel RF 2328
Salut,
courroies crantées ou pas, la longueur est-elle la même 
si oui,
la démarche pour les calculs doit-être la même…
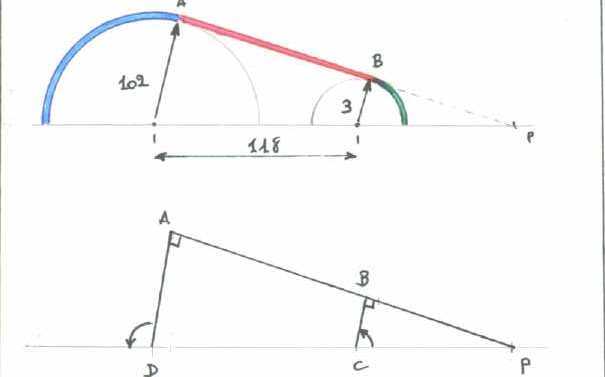
Pour ceux que ça intéresse, voici le développement géométrique. 
[/img]
Pour simplifier, calculons la demi-courroie (d’où les coefficients « 2 » dans la formule de Jacques).
Les deux rayons représentés rejoignent la tangente perpendiculairement, donc sont parallèles entre eux. Monsieur Thalès (rien à voir avec Thomson !) nous dit :
PC / PD = AC / BD = 102/3 = 34 → PC=34PD
Or, PC - PD = 118 donc PD = 3,6 → PD = 121,6
Interviewons maintenant Mr. Pythagore :
PC² = PA² + AC² → PA = racine de (121,6)² - (102)²
PA = 66,2 De la même façon PB = 2 → AB = 64,2 mm
(partie rouge)
En voilà déjà un bout. Ensuite tg PDB = 2/3 → PDB = 33,7°. Longueur de la (demi) courroie tangente à la petite poulie : l = 2.Pi.r x (33,7/180) = 1,8 mm (partie verte)
Même raisonnement du côté de la grande poulie, mais cette fois ce qui nous intéresse c’est l’angle supplémentaire (soit 180° - 33,7 = 146,3°) qui nous donne une longueur de (demi) courroie tangente à la grande poulie de 260,4 mm.(partie bleue)
Au total, en multipliant par 2 pour la courroie entière :
2 x (260,4 + 64,2 + 1,8) = 652,9
La petite différence avec le résultat de Jacques vient je pense de l’erreur introduite par la notation « calculatrice » de l’angle (33,7° et 146,3°) qu’en toute rigueur j’aurais dû convertir en minutes.
En ce qui concerne la correction du diamètre, tout dépend de la cote indiquée dans le catalogue. Le mien donne le diamètre intérieur de la courroie. Il n’est donc pas nécessaire d’ajouter le demi-diamètre (ou épaisseur) de la courroie. Peut-être que d’autres catalogues donneraient une dimension moyenne au niveau de l’axe ? Pas sûr.
Désolé pour le smiley « cool » 8) qui est venu se glisser dans la totalisation finale. Bien entendu il faut lire « 8 » à sa place, soit 1,8.
Pour ceux qui veulent vérifier si ma formule est juste, voici ci-joint une petite démonstration rapide ci-joint (au format word).
PS: Je voudrais bien insérer des images dans le texte de ce forum mais je ne sais pas comment on s’y prend.
Y aurait-il quelqu’un qui sait?
Merci.
Courroie.doc (33.5 KB)
Bonjour à tous.
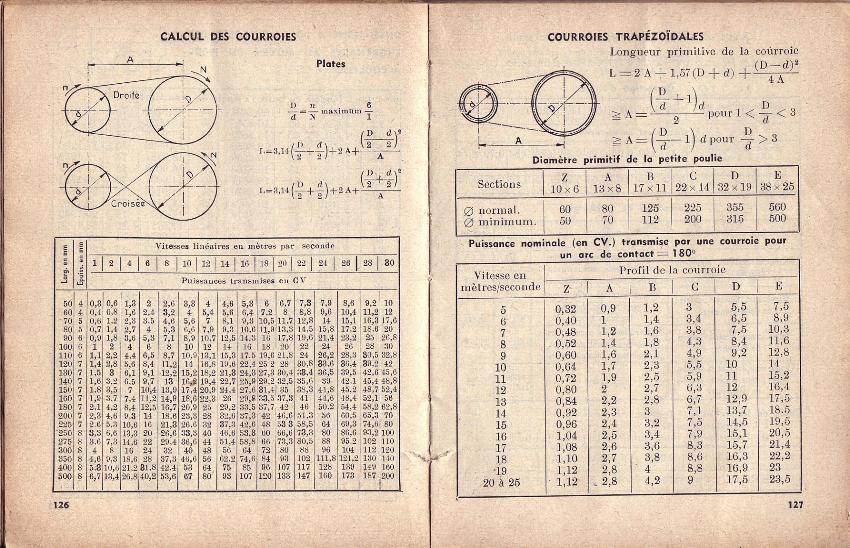
Voici une photo qui devrait vous éclairer sur la façon de calculer la longueur d’une courroie (plate, trapézoïdale.) Et sinon vous avez la solution de la ficelle que vous passez dans le fond de gorge, vous tendez la ficelle, vous la coupez, sur le bord extérieur de la poulie vous faites la même manipulation, vous mesurez les deux brins, vous faites une soustraction, vous divisez le résultat par deux et vous l’ajoutez au brin le plus court ou bien vous le soustrayez au brin le plus long, (ceci est valable que pour les courroies trapézoïdales ou rondes.) Pour les courroies les plates ou courroies crantées une seule mesure suffie.
Alain.
Merci beaucoup M. Greuet, c’est la formule que je cherchais depuis des mois !
Je vais l’archiver soigneusement.
Daniel Bélanger
Bonjour à tous,
Réactualisation d’un sujet ancien.
Ci-dessous, un tutoriel en images pour mesurer, définir et approvisionner un grand nombre de courroies utilisées dans nos appareils électroniques anciens + l’adresse d’un site où le rédacteur de l’article s’approvisionne.
Merci ! à Jelora.
Cordialement
jhalphen
Courroies en tous genres :