constantes de temps

Technique
1

Bonjour,

Voir schéma joint.

Pendant leur phase de charge, je cherche à évaluer un ordre de grandeur de la constante de temps des deux circuits RC ayant chacun pour condo :

  1. C13, 100 pF, le condo de détection MA. Il se charge depuis le secondaire de MF2 via l’une des 2 diodes de l’EBF2,
  2. C16, 47 pF, le condo de « liaison » vers le circuit de CAG. Il se charge depuis le primaire de MF2 via l’autre diode de l’EBF2.

En fait, je cherche à savoir comment évaluer la résistance (l’impédance) en série avec chacun de ces 2 condos pendant leur phase de charge :
C13 : est-ce l’impédance présentée par le secondaire de MF2 ?
C16 : est-ce l’impédance de sortie de l’ampli MF ?

Pendant leur courte phase de décharge (une portion de période du signal MF) : 1. C13 se décharge en gros dans Pot. 2 : constante de temps = 100 pF x 500 k? = 50 µs 2. C16 se décharge en gros dans R11 : constante de temps = 50 pF x 1 M? = 50 µs.

Ces valeurs de C et R sont très classiques mais pourquoi diable des valeurs différentes pour les C et R ?
Y’a un truc ?
détection - CAG.jpg

2

la constante de temps To = R X C ne correspond pas à la charge. Le temps de charge équivaut à environ 5 X To, peut être est ce là le pB ?

3

Bonjour Philippe,

Oui bien entendu (pour l’estimation du temps de charge).
Mais ce que recherche, c’est un ordre de grandeur de R pour chacun des 2 condos.
:wink:

4

Il faut voir plutôt leur impédance à le fréquence de 480 kHz… ces condensateurs sont là pour éliminer les fréquences résiduelles FI pour ne garder que la composante BF 300 Hz à 10.000 Hz.
Pour exemple, l’impédance de ce type de condensateur 100 pF appelé aussi capacitance est de 3500 ohms à 450 kHZ.
En matière de constante de temps symbole lettre grecque téta ou T = RC. Il faut 5 T pour charger un condensateur ,même temps pour déchargement.
Voir éventullement Formulaire de la radio de W.Sorokine … que l’on peut encore trouver sur le WEB.
Jacques DUDORET

5

J’ai oublié les unités : T = seconde, R = ohms, C = Farad d’où 1 µF = 1 * 10 puissance -6, 1 pF = 1 * 10 puissance -12, 1 nF = 1 * 10 puissance -9. Il faut assimilé que l’écriture 10-² veut dire 10 puissance -2. Nous n’avons pas sur un clavier de PC la possibilité d’une telle écriture. Nous n’avons que l’exposant « 2 », première touche à gauche, second rang.
Jacques DUDORET

6

Bonsoir,

Jacques,
Merci de vos interventions.
Pas de problème ici pour calculer les réactances capacitives.
Si C13 (le condo de détection MA) élimine effectivement la porteuse FI pour ne garder que la composante BF (10 000 Hz, ce serait bien !), il n’en est pas de même pour C16, le condo de « liaison » vers le circuit de CAG. En effet, C16 permettra au contraire de ne conserver que la porteuse FI.

En matière de constante de temps, le symbole consacré est la lettre grecque tau : ? tandis que ?, thêta, est plutôt utilisée pour les températures ou les angles.

Pas de problème pour les formules de charge et décharge des condos.

Pour les exposants, un usage répandu est d’utiliser le signe ^ : 10^3, 10^-12, (a² + b²)^1/2, etc.

Bref, ma question n’était pas là…
Ma question était : quelle est l’impédance série qui permet de charger mes 2 condos ?
:wink:

7

Bonjour,

Pour le CAG, la constante de temps doit être plus grande que celle de la cellule RC de la BF, cela va de soit, de l’ordre de la fraction de seconde.

Il serait bien d’ailleurs de l’augmenter également de nos jours sur l’ oeil magique, avec la généralisation de la modulation DCC en.m.wikipedia.org/wiki/Dynamic_ … _using_DCC (en lieu et place de l’AM traditionnelle à puissance de porteuse fixe) sur les émetteurs actuels, il se transforment maintenant en vu mètres :wink:

8

Bonjour,

Henri-Louis,
Merci pour votre intervention.

Dans le circuit du CAG, le condensateur C16 dont je recherche l’évaluation de la valeur de la résistance série de charge n’est pas le condensateur participant à la constante de temps du CAG.
En effet, les constantes de temps propres à la CAG sont définies par R12C18 et R13C19 qui donnent des valeurs tournant autour du dizième de seconde.

Je pense que la R de charge de C16 est constituée par la mise en // de la « résistance » interne de la pentode avec la « résistance » présentée par le primaire de MF2 (à la résonance).

9

Bonsoir,

Bon, je vais prendre 1 problème à la fois.

Condo de détection, voir nouveau schéma simplifié joint, phases de charge (en vert).
Je cherche à savoir à travers quelle résistance (impédance) ce condo se charge.

Serait-ce à travers l’impédance présentée par le secondaire de MF2 (+ la résistance interne de la diode) ?
Mais cette impédance présentée par MF2 est forte, genre 175 000 ohms.
Ce qui donne une constante de charge très élevée devant 1 µs.
Alors que la tension aux bornes du condo semble suivre la porteuse MF.

Avant que je ne me lance dans un Thévenin de la pentode + MF2 ! :unamused:

Pour MF2 : F=455 kHz, Q=100, L=611 µH, C=200pF.
MA_charge condo détection_r.jpg

10

Bonjour
J’avais des problèmes avec un Pathé435L , la BF passait dans la CAG .
viewtopic.php?f=2&t=235416
Si l’on fait les essais avec un géné. HF modulé , tout va bien , ce n’est plus le cas avec les modulations actuelles de certains émetteurs .

11

« …la tension aux bornes du condo semble suivre la porteuse MF »
Cette rapidité à suivre la tension du secondaire n’est elle pas simplement due à la mise en parallèle du condensateur de 100pF avec le condensateur du circuit accordé ?
Mise en parallèle quasi instantanée des 2 condensateurs par la diode. Il n’y aurait que la résistance directe de la diode qui retarderait l’égalisation des tensions entre ces 2 condensateurs.

12

Bonjour Jean-Claude,

Ah oui, ce n’est pas bête du tout cette façon de voir !
Je me disais d’ailleurs que ce fichu condo de détection (100 pF) devait sacrément dérégler l’accord du secondaire…

Mais 100 pF en plus en //, c’est quand même beaucoup par rapport au propre condo du secondaire (celui qui est dans le boîtier) et qui a une valeur de l’ordre de 200 pF.

La littérature est fort discrète sur cette affaire.

D’un autre côté, cette mise en // n’a lieu que pendant les temps de conduction de la diode et ces temps vont dépendre des caractéristiques de la BF (fréquence, amplitude) et du taux de modulation : ça se corse !

13

Ayant encore trop en mémoire une autre discussion, j’ai hésité à donner mon point de vue personnel sur ce présent sujet. J’ai finalement décidé de la faire, en soulignant une nouvelle fois, que c’est un point de vue personnel que personne n’est forcé de partager.

La question est donc de connaitre la résistance interne de la source alimentant le circuit redresseur utilisant la diode du haut. Ai-je bien compris cela ?

Si oui et si nous pouvons nous limiter au cas du circuit à la résonance, nous pouvons commencer par éliminer tous les éléments réactifs, car leurs susceptances se compensent mutuellement. C’est d’ailleurs ainsi que se définit la résonance, n’est-ce pas ?

Le circuit en question est connecté au primaire du transformateur. Le secondaire n’exerce donc son influence que par la transformation qu’effectue le transformateur. Au secondaire, nous trouvons l’autre circuit redresseur avec toute sa quincaillerie derrière, qui amortit le secondaire. Cela conduit donc à un amortissement supplémentaire du primaire, déjà amorti par les pertes du circuit accordé et par la résistance interne du tube. Il y a donc ces trois choses, que je mettrais toutes en parallèle. Oui, toujours ma flemme. Par ailleurs, nous avons le tube considéré comme source de courant. Tout cela transformé à la sauce Thévenin, nous donnera une source de tension avec cette résistance interne recherchée en série.

Attention pourtant ! D’abord parce que cette transformation du secondaire avec sa quincaillerie derrière, ne peut pas être faite comme si le transformateur était parfait. Ensuite parce que toutes ces choses-là varient avec le niveau du signal. Le redresseur au secondaire amortit davantage le circuit aux niveaux faibles. Le tube, soumis au CAG, aura un courant plus important aux niveaux faibles, sa résistance interne diminuera, amortissant davantage le primaire.

Bon ! Tout ça est un début de réflexions, pas une solution analytique finale, ni un ensemble de formules toutes prêtes à l’usage.

Mais si ça peut faire avancer un peu le schmilblick…

Douces salutations pas plus avancées pour autant !

14

Bonsoir Souris blanche,

Très content de vous lire.
Je suis arrivé exactement aux mêmes conclusions que vous.
C’est fou ce que ces quelques composants peuvent entraîner comme calculs déments.

Sturley (tome 1, à partir de la page 339) a d’ailleurs fait une étude pratique et mathématique très poussée
sur les divers causes et conséquences de l’amortissement du secondaire.
Mais je n’ai pas vu d’études sur le sujet qui me polarise pour le moment.

J’ai fait le calcul du générateur équivalent de Thévenin, vu du secondaire de MF2, en partant du circuit anodique de la pentode (donc son impédance interne ?), dans le cas particulier suivant :
L1 = L2 = 611 µs
C1 = C2 = 200 pF
(f = 455 kHz)
r1 = r2 (r effective série des CO) = 17,5 ?,
en exprimant le résultat de l’impédance Thévenin en fonction de la résistance interne de la pentode ?, du coefficient de couplage k et du facteur de qualité Q.
Ca donne une jolie expression complexe après une bonne prise de tête…

En prenant k = 0,01 (donc pas loin du couplage critique, kQ = 1), voici ce que ça donne :

Z= (? + rQ²) / [k + (k² + 1/Q²)(?/r)], au voisinage de la résonance.

Avec ? = 1M?
r = 17,5 ?
k = 0,01
Q = 100,
ça donne environ 95 k?, disons 100 k, soit une constante de temps de 10µs (C_détection = 100 pF), ce que je trouve grand devant la demi-période (1 µs) du 455 Hz…

Jean-Claude Jardiné a une suggestion intéressante : voir son intervention plus haut. C_détection ferait partie du condo du CO secondaire.
Voir aussi ma réponse à ce sujet.

Très impatient de lire vos commentaires.

15

Bonjour M. Waymel,

Je retrouve là votre tendance à tout vouloir mettre en équation. :slight_smile: Mathématiquement très intéressant, je le reconnais, mais il me reste des doutes importants quant à la portée pratique. Comme l’influence du niveau du signal est important, cette fameuse résistance interne va varier beaucoup. Il faudrait alors reconsidérer les choses pour divers niveaux de signal. Cela fera-t-il vraiment avancer le schmilblick ? Hmm… :confused:

Même si le schéma que vous indiquez est très, très classique, ce n’en est pas moins du bricolage économique pour réduire les coûts de fabrication. Un circuit de CAG sérieux est quand-même fort différent. Il suffit d’étudier un peu les schémas de récepteurs de trafic.

J’avais déjà lu cet échange de messages et je reconnais humblement ne pas partager cet avis.

Les choses ne sont pas si simples. Le premier et grand problème est que nous avons considéré les choses, jusque là, sous la supposition que tout était linéaire. Si cela ne l’était pas, nous avons essayé de transformer le réel en quelque chose qui pourrait sembler linéaire. C’est surtout avec le circuit de détection que nous avons fait ainsi en essayant de trouver l’amortissement qu’il provoque, ce qui revient à en déduire une simple résistance, alors que nous savons fort bien que ce circuit est non linéaire par sa nature même. Tout cela est très compréhensible et très commun car sinon il faudrait se lancer dans des calculs de circuits non linéaires et alors là, nous ne sortirions pas de l’auberge de si tôt. Je possède un petit bouquin où l’auteur se lance dans une telle aventure, mais je préfère ne pas m’engager sur cette voie.

L’idée de M. Jardiné consiste à considérer que la capacité de charge de la détection se joint temporairement (durant une partie du cycle) à la capacité du circuit accordé du secondaire. Je ne mettrais pas en doute que cette façon de voir est exacte, mais je n’entrevois vraiment pas comment on pourrait traiter cela mathématiquement sans se lancer dans des constructions vraiment très complexes. Pour une simulation en mode « transient », cela ne pose pas de problème, bien sûr. Mais ça aussi, c’est une autre affaire.

Pour les vrais matheux, de tels développements fort complexes seraient probablement un régal. J’avais une camarade de travail qui s’en lècherait les babines. Personnellement, je ne désire jamais couper le lien avec la réalité de ce que nous analysons ici. Nous devons aussi nous souvenir qu’un récepteur de radiodiffusion est un bidule plein de compromis un peu partout. Le but à atteindre est d’obtenir un résultat à peu près acceptable à un niveau de complexité limité, conduisant à une fabrication non critique, à un prix de revient fort modeste.

Tout cela est un point de vue très personnel, bien sûr. :slight_smile:

Douces salutations sans complexité !

16

Bonjour à tous,

A Souris blanche,

J’avais oublié de vous répondre : c’est la diode du bas, celle de la détection.
Pour la diode de CAG, ce sera après !
Mais vos propos traitant aussi de la diode de détection, je m’y retrouve !

A nouveau tout à fait d’accord !
Il est exact que j’adore les « récréations mathématiques ».
:wink:

D’un autre côté, mon objectif de base est toujours le calcul des valeurs des composants d’un poste classique.
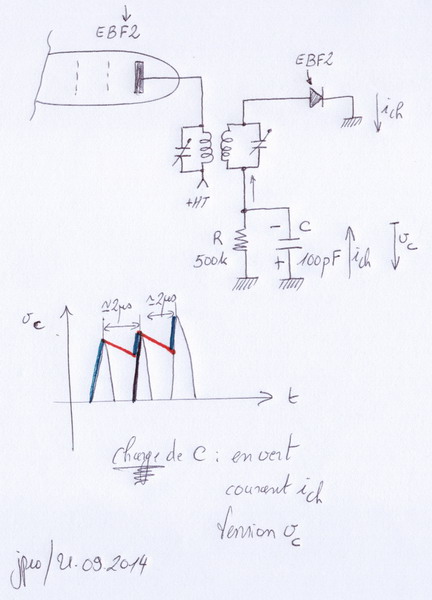
Aussi, quand je suis arrivé sur le condo de détection Cd et la résistance Rd, j’ai d’abord essayé de comprendre comment ça marchait en pratique puis j’ai estimé la constante de temps de décharge par simple multiplication de Rd par Cd. Pour cette décharge, pas de problème, ça collait avec un 100 pF et une 500 k? : 50 µs.

Pour la charge de Cd, afin que le signal issu de la détection suive au mieux les montées (en valeur absolue) du signal MA, j’ai conclu que la constante de temps devait être petite devant le quart de la période de la porteuse. Donc pour du 500 kHz (j’arrondis), inférieure à 0,5 µs et que par conséquent la « R série de charge » devait être inférieure à 5 k?.

Ma première idée a été de dire que cette R était constituée par la R effective série du CO (ici 17,5 ?) en série avec la résistance interne de la diode passante.

Mais un regard plus aigu m’a fait voir que c’était l’impédance // du CO qu’il fallait prendre en considération.
Soit Q² fois plus : 175 000 ? !
Je me suis alors lancé dans des calculs monstrueux (80 pages, à force de les refaire…).
Pour arriver à une formule où j’avais mis l’impédance interne de la pentode en paramètre.

On arrivait toujours à des valeurs importantes de l’impédance qui « chargeait » Cd.
Normal après tout, c’est un CO // déjà pas mal amorti certes (d’où le couplage un peu plus serré pour ce transfo MF2 par rapport à MF1, je suppose).

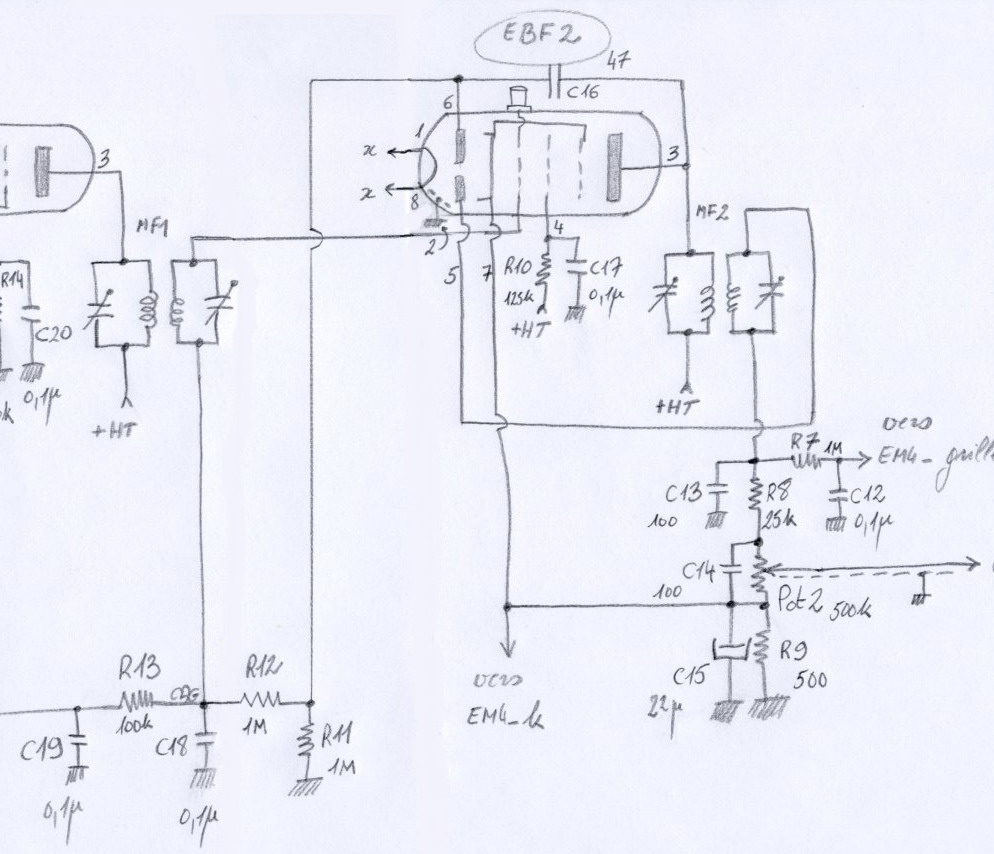
Jean-Claude Jardiné est alors intervenu pour me faire voir que « physiquement » Cd venait s’ajouter au condo du CO du secondaire de MF2 (ajout //).
Imparable quand on regarde le schéma.
Ce qui expliquerait parfaitement que la tension aux bornes de Cd suive le signal MA pendant la phase de charge de Cd.
Et l’impact énorme de 100 pF (Cd) en // sur 200 pF (le condo du transfo) serait minimisé par les faibles temps de conduction de la diode.

On entre effectivement dans le non-linéaire. Bon, ben ça m’intéresse encore plus (à titre de récréation).
Je suis donc intéressé par les références de l’ouvrage que vous évoquiez…

PSPice doit bien le faire ce fichu calcul…
Au passage, sans Cd ni Rd, j’arrive à une impédance vue du secondaire de MF2 égale à… 10 k? !!!
C’est la résistance qu’il faut mettre en // sur le secondaire de MF2 pour diviser sa tension à vide par 2.
Et là, nouveau mystère…

Enfin, pourquoi le couple 500 k? /100 pF pour Rd / Cd et pas un autre si leur produit fait 50 µs (pour la décharge de Cd) ? Pourquoi pas 1 M? / 50 pF voire 2 M? / 25 pF ? Ca dérèglerait moins le CO secondaire…
Toujours dans l’idée de « calculer » les valeurs des composants d’un poste classique.

17

En fait, ces valeurs-là constituent le compromis classique que l’on retrouve un peu partout.

Václav Doležal: « Non linear networks ». Elsevier 1977.

C’est un vieux prof qui m’a donné ce bouquin avant de partir à la retraite. L’auteur semble être un expert en cette matière. Avis aux amateurs !

Bien sûr, mais c’est un outil de simulation, qui a une tâche différente, bien plus simple.

Comme je l’ai écrit, c’est le compromis classique. Les raisons de ce choix sont expliquées dans certains des bouquins classiques, dont nous avions déjà parlé. Je ne sais plus lequel l’explique le mieux. Faudrait voir. Je commencerais pas le Sturley. Il y a des lambeaux qui traînent dans ma mémoire…

Dans la manière de faire que j’avais expliquée, j’étais partie du cas de la résonance, ce qui m’a permis d’omettre tous les bidules réactifs, car ils s’annulent à la résonance. C’est très pratique. Je n’étais pas encore allée au bout de mes réflexions, car je ne suis pas sûre que le secondaire, à la résonance, n’introduise pas quand-même encore une réactance inductive vers le primaire. Quant au rapport de transformation de l’impédance au secondaire vers le primaire, ce n’est pas le même que celui qui résulte directement du nombre de tours des bobinages. J’avais l’idée d’utiliser un circuit équivalent comprenant, en autre, un transformateur parfait. Ce serait peut-être pratique ici.

Ce sont juste quelques idées. Je ne m’apprêtai pas à me lancer moi-même dans ces calculs. Peut-être pourront-elles vous être utiles d’une façon ou d’une autre.

Mais je voulais quand-même encore rappeler ma remarque à propos de l’importante influence du niveau du signal.

Je vous souhaite bon succès dans votre entreprise.

Douces salutations compromises !

18

re-,

Oui je suis en phase (ça tombe bien !).
Je m’en vais de ce pas rechercher le livre indiqué.
Merci pour la référence, avec les petits signes diacritiques (?) qui vont bien…

J’ai repéré beaucoup de pages dans les bouquins sur l’influence de l’amplitude des signaux (détection), surtout dans le Sturley, effectivement.

Mais maintenant, il faut que je finisse mon support de stage, la date approche !
Je reprendrai mes petits calculs un peu plus tard. :frowning:

So long (mais je risque de revenir pour l’autre diode : la CAG…)…

19

Bonsoir,

Ayant fini le support pptx du stage du week-end prochain, j’ai repris mes petits calculs…

J’ai donc fait le Norton de MF2 vu du secondaire non chargé.
Cette fois-ci, comme Souris Blanche me l’avait conseillé à plusieurs reprises, j’ai opté pour un calcul « tout parallèle ».
L’admittance Norton obtenue est égale à l’admittance du CO // secondaire : 1/(Qs² x rs) + un terme plus complexe représentant l’admittance du CO // primaire et l’admittance du circuit anode de la pentode ramenées au secondaire.

Ce soir, je scannerai la ch’tite formule…
formule générale en PJ
CP : u = 0 (on enlève la source), L1 = L2 = L, C1 = C2 = C, r1 = r2 = r, ? = ?0, kQ = 1 (couplage critique),
on obtient y = Y2+Y1.
Comme Y1 = Y2 = Y, on a y = 2Y ou z = 1/y = Q²r/2.

A Q²r du CO secondaire vient s’ajouter en // Q²r ramené par le CO primaire au couplage critique pour faire l’intégralité de l’impédance vue du secondaire de MF2. Logique…
Mais ce n’est qu’un cas particulier !
Norton MF2_r.jpg