Doctsf (Modèles & Marques)
AnnoncesUn ptit dernier pour finir la soirée!
Apparemment il y a une notion qui vous échappe c’est celle de rareté !
Truc connu …
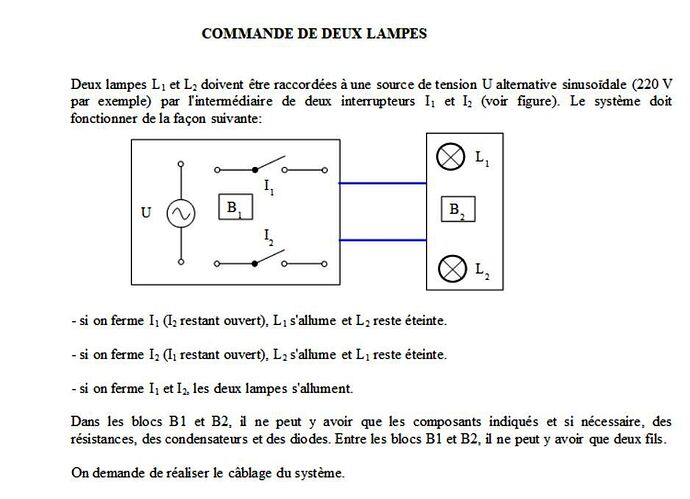
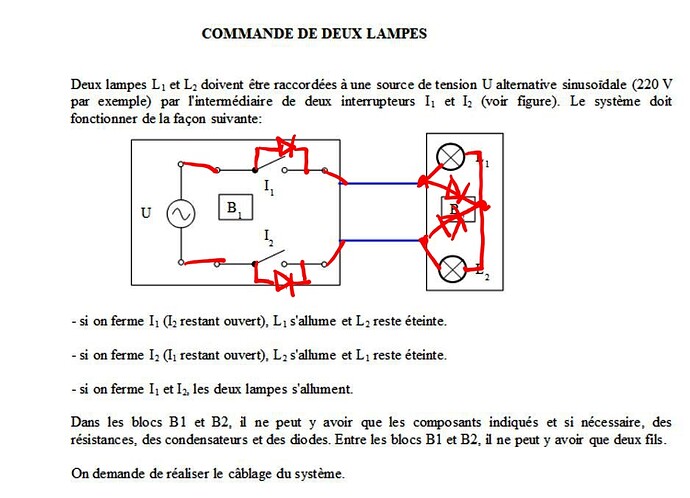
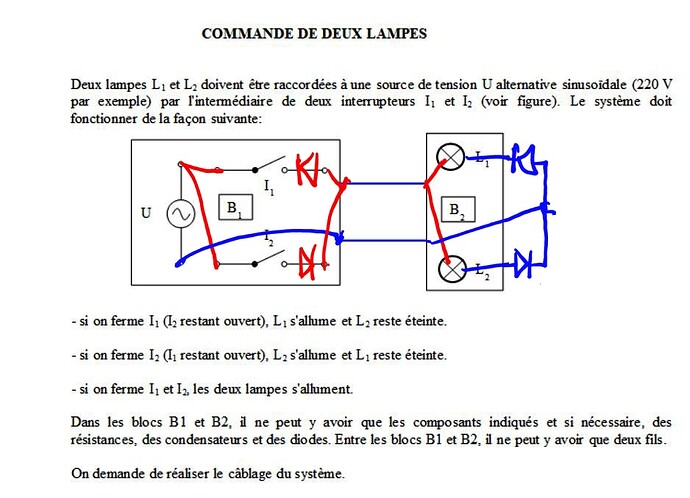
Une lampe sur l’alternance positive une lampe sur l’alternance négative, j’ai réalisé de manière pratique cela pour faire allumer des lampes de signalisation avec seulement deux fils à disposition.
On peut également faire la même chose en parallèle plutôt qu’en série.
2 « J'aime »
Y a du souci à se faire …
Ce problème nous donne une excellente occasion d’appliquer le théorème de Bernard Tellegen (celui qui a aussi inventé la grille de suppression).
@Nuage de quel problème parlez vous ? Il y en a eu plusieurs dans ce fil. Ceci dit c’est un peu tous les même sauf le dernier …
Veuillez excuser mon imprécision, SVP. Je voulais parler du problème du potentiomètre.
@Nuage Probablement si on raisonne en terme d’énergie. Pour ma part j’ai juste considéré l’expression d’un diviseur de tension constitué d’un résistance R' en série avec deux résistances parallèles R'' et R puis en utilisant R_{pot}=R'+R'', soit :
U_R=\frac{\frac{1}{\frac{1}{R''}+\frac{1}{R}}}{R'+\frac{1}{\frac{1}{R''}+\frac{1}{R}}}U après quelques manipulations algébriques on obtient :
U_R=\frac{R''R}{R'R''+RR_{pot}}U soit U_R=\frac{R''R}{(R_{pot}-R'')R''+RR_{pot}}U puis on extrait de cette l’équation du second degré R''. Avec les valeurs numériques proposées, l’équation du second degré se réduit à R''^2=RR_{pot}.
1 « J'aime »
Oui, je vous comprends bien et c’est probablement là l’idée qui nous vient d’abord à l’esprit. Ce n’est d’ailleurs qu’avec du retard, que l’idée d’utiliser le théorème de Tellegen (trop souvent oublié) m’est venue. Mais c’en est une belle application, à mon avis.
Bonjour,
2R/2R =1
Bonjour.
Attention ce n’est pas 2R/2R, mais 2R//2R.
@Nuage Je viens de regarder le développement par Tellegen, ça a l’air un peu plus compliqué car c’est une équation en \frac{V^2}{\Omega} à résoudre au lieu d’une équation en V. Je n’ai pas été jusqu’au bout. Si vous avez le développement, je suis preneur.
Rx=1020 \Omega environ ?
Je pars du curseur du potentiomètre, que je considère comme nœud.
(50 - R’) - 50/(100 - R’) - 1 = 0
Le courant qui y entre est égal au courant qui en sort. En fait, c’est déjà selon Gustave Kirchhoff.
Aïe ! Nous ne connaissons pas la phase de ce courant de 0,1 A.
La phase du courant est une des deux inconnues obtenues lors de la résolution. Pour ma part, j’obtiens une phase pour le courant de 0,8088 rad.
Je ne comprends pas votre formule, voulez-vous dire :
50-R'-\frac{50}{100-R'}-1=0 c’est à dire : 49-R'-\frac{50}{100-R'}=0. Le 1 serait homogène à des \Omega ?
Non, c’était faux ! 1000 Zexcuses !
(50 / R’) - 50/(100 - R’) - 1 = 0
1 est le courant dans la charge 50 V sur 50 Ω.
1 « J'aime »
En effet, ça donne bien la même chose. C’est assez élégant comme approche. Merci