Sans vouloir critiquer la valeur des résultats obtenus avec PSUD2, ce qui me dérange est que ce soit un logiciel propriétaire fermé, ne roulant que sous M$-Windows. On ne peut pas apprécier les algorithmes utilisés, on ne peut pas les changer, ni les améliorer, en cas de besoin.
C’est certain, le régime à peu près stable ne s’établit qu’avec le temps. Plus la résistance de la source est grande et plus la capacité est grande, plus ça dure. Finalement, il faudra vérifier que les diodes puissent encaisser le fort courant à l’enclenchement, lorsque le condensateur est complètement déchargé.
Cela ne me surprend guère d’apprendre cela, car cela simplifie bien des choses. La question reste posée: Est-ce là une approximation valable en pratique, comme Larass semble le suggérer ?
Bonjour,
Ce n’est certainement que PSpice avec un éditeur de schémas et une présentation des résultats différentes, au contraire de LTSpice qui lui est très ouvert.
Cela m’étonne, car je ne connais qu’une version pour M$-Windows et une autre pour Apple Mac.
Bonjour
De nombreuses versions open source de Spice existent.
Le code original de Spice a toujours été public, il a été ensuite accomodé à la sauce pro ou interface graphique, mais ça ne change rien au coeur du logiciel.
Ça c’est vrai pour spice, mais pas pour LTspice. J’utilise spice depuis de nombreuses années déjà, mais pas LTspice.
Dès que je termine le programme pour itérer sur un nombre quelconque d’alternances, je peux vous l’envoyer en plus des formules analytiques. Une petite modif permettra d’introduire le modele simplifié de Larass pour comparaison.
Probablement d’autant plus valable que l’ondulation résiduelle est faible!
Mr de la Palisse l’aurait dit!
N’avons-nous vraiment rien oublié ?
Voici le programme qui permet d’itérer sur plusieurs alternances.
Il est possible de modifier les valeurs la charge Rl, le condo C, la résistance interne de la diode Rs.
On peut aussi modifier le seuil de conduction de la diode.
close all
Rs=100;
Rl=1000;
C=47e-6;
f=50;
w=2pif;
U0=100;
b=Rs^2C^2w^2Rl^2+(Rs+Rl)^2;
u0=0;
tb=0;
ntb=1;
n=4;
PasTemporel=1e-6;
for k=1:n
t=(k-1)/f:PasTemporel:(k+1)/f;
U=U0sin(wt);
u=U0Rlexp((Rl+Rs)(tb-t)/Rl/Rs/C)(RsRlCwcos(wtb)-(Rs+Rl)sin(wtb));
u=u-RsRlRlCwU0cos(wt)+Rl(Rs+Rl)U0sin(wt);
u=u/b;
u=u+u0exp((Rl+Rs)*(tb-t)/Rl/Rs/C);
hold on
plot(t(ntb:end),U(ntb:end),‹ b ›)
utc=U(ntb:length(t))-u(ntb:length(t));
lconduit=ones(1,length(t));
lconduit(ntb:length(t))=utc>0;
ntc=find(~lconduit,1);
plot(t(ntb:ntc-1),u(ntb:ntc-1).*lconduit(ntb:ntc-1),‹ r ›);
tc=t(ntc);
v=u(ntc)*exp(-(t-tc)/Rl/C);
vtb=U(ntc+1:length(t))-v(ntc+1:length(t));
lbloque=zeros(1,length(t));
lbloque=vtb<0;
ntb2=find(~lbloque,1);
plot(t(ntc:ntc+ntb2),v(ntc:ntc+ntb2),‹ r ›);
tb=t(ntc+ntb2);
u0=v(ntc+ntb2);
ntb=ntc+ntb2-floor(length(t)/2)
end
grid
xlabel(‹ t (s) ›);
ylabel(‹ V ›);
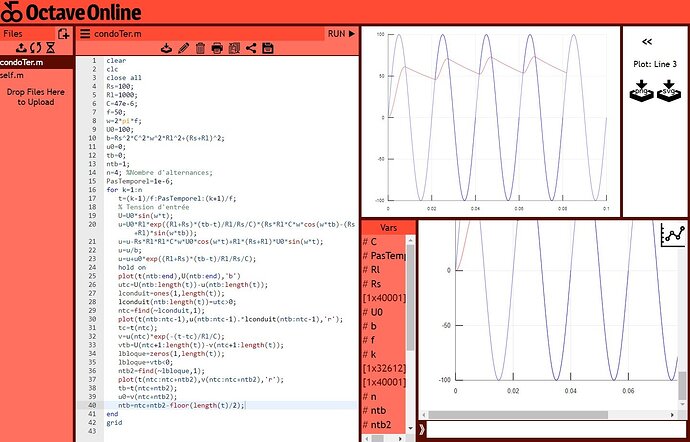
Programme qui peut être exécuté sur octave online (https://octave-online.net/)
Voici le rendu
L’EZ80 semble correspondre à à Rs=300 \Omega.
Certaines * du programme ne semblent pas passer sur cette page (il y a la capture d’écran pour corriger ce qu’il manque)
@Nuage Pour pouvoir évaluer la technique de Larass, il manque une information qui n’est pas sur la figure du premier post.
Les courants de charge et de décharge sont constants dans ce modèle simplifié mais que valent-ils ?
Le développement mathématique qui va avec donne-t-il \hat{I} et I_0 ou encore les pentes des droites ?
Si on modifie le programme pour mettre des fonctions affines pour la charge et la décharge du condo, on obtient rapidement ceci.
Ici j’ai mis un courant de charge correspondant à U0/Rs et un courant de décharge correspondant à U0/Rl. C’est purement arbitraire, je pense que Larass a du être un peu plus finot pour choisir ces deux courants qu’il a supposé constants. Faudrait voir son bouquin.
Merci @Stockfish ! Je vous ai envoyé le scan du chapitre de Larass, du livre de Wagner, dans lequel j’avais trouvé la méthode.
D’après les courbes, que vous avez produites, il y a quand-même une différence non négligeable entre les deux méthodes.
La différence est due au fait que j’ai pris des courants constants un peu au pif. D’après le bouquin, on a bien un courant de décharge I0 = U0/Rl ça ca semble normal, les pentes de décharges correspondent donc bien à la figure produite par le prog. Ce sont les pentes de charges qu’il faut revoir. D’après ce que j’ai compris, la première serait bonne, ce sont les suivantes qu’il faut revoir. Une chose est sure elles sont moins raides.
Je crois que c’est bon cette fois-ci pour Larass. Il a bien pris I_0=\frac{U_0}{R_l} pour la décharge donc il considère que le condo est chargé au max et pour la charge, il considère I=\frac{U_0-u(tc)}{R_s} ce qui paraît logique aussi.
Voici ce que ça donne :
L’écart se manifeste principalement sur l’ondulation résiduelle donc comme disait ON5WF plus elle est faible meilleur est le modèle sans doute. On observe que la tension basse converge bien vers la valeur exacte. C’est la tension haute qui est surévaluée. Faudrait ajouter une self derrière pour voir …
Qui s’y colle ?
Petit problème de couleurs entre la légende et les courbes.
oui, j n’ai pas trouvé le bug …
En fait, le seul intérêt de de la technique de Larass c’est de pouvoir représenter la fonction u(t) à l’aide d’une règle et d’un compas comme au temps d’Euclide ! (le compas et la règle pour la fonction sinus) la règle pour la tension u aux bornes du condo. Donc c’est plus rapide qu’avec une règle à calcul si on se replace dans le contexte des années 50. Mais aujourd’hui avec une simple calculatrice scientifique telle que la HP-35 sortie en 73 ce n’est plus du tout d’actualité. Il faut bien sur conserver ce bouquin pour sa dimension historique mais ne pas utiliser ce qu’il contient. On a mieux aujourd’hui.
La résolution purement analytique c’est à dire obtenir l’ondulation résiduelle en fonction de la valeurs des composants nécessite la résolution d’une équation algébrique du type at+b=U_0\sin{\omega t} ce qui est tout aussi impossible que la recherche analytique de la solution exacte de Waidelich.
Oui, car même s’il y a des « couteaux suisses » qui font tout ça, il faut quand même comprendre ce qui se passe!
En général, en tout cas dans les ouvrages que j’ai, l’(es) auteur(s) considère(nt) que le régime permanent est établi; est-ce le cas chez Herr Larass?
 Doctsf (Modèles & Marques)
Doctsf (Modèles & Marques) Annonces
Annonces