Bonjour,
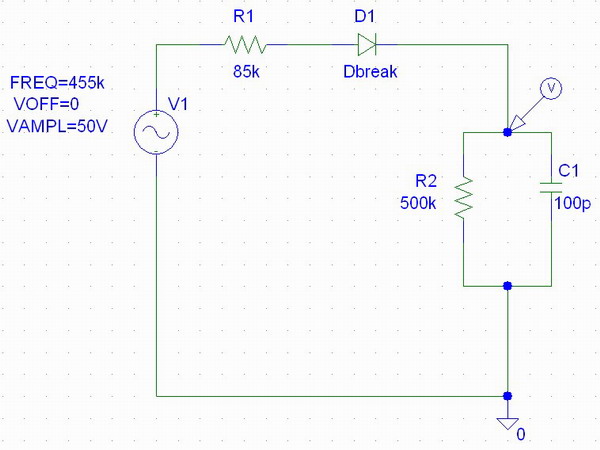
Voir la simulation PSpice jointe.
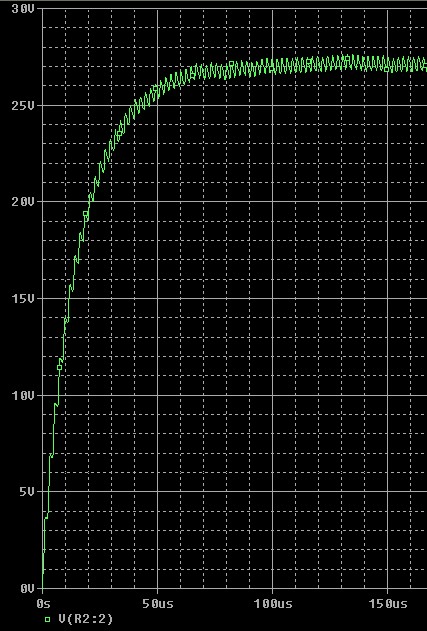
J’avoue ne pas savoir actuellement retrouver par le calcul la valeur de la tension de sortie (environ 27 V).
Une piste ?
Merci.
Bonjour,
Voir la simulation PSpice jointe.
J’avoue ne pas savoir actuellement retrouver par le calcul la valeur de la tension de sortie (environ 27 V).
Une piste ?
Merci.


Bonsoir,
Je crois bien qu’il n’ y a pas de solution simple a ce problème parce que :
D1 Bloquée : La décharge du condensateur à travers la résistance est exponentielle.
D2 Saturée : La charge du condensateur se fait par un arc de sinusoïde à travers un pont diviseur. C’est à dire trigonométrie + calcul infinitésimal.
Les 2 sont liés et pas de simplification en vue. Il y a peut être des méthodes approchées, des tables, des abaques…
Tx
Bonjour,
Le problème est extrêmement compliqué et à part la simulation, je ne pense pas que le calcul soit possible.
En gros…
La « loi des noeuds » est valable pour les valeurs moyennes. Le courant moyen dans dans un condensateur est nul (en régime établi). On en déduit que le courant moyen dans R1 est égal au courant moyen dans R2.
Les tension moyennes entre R1 et R2 se répartissent donc dans le rapport des résistances (comme dans un montage potentiométrique).
La ou ça coince, c’est que la tension aux bornes de R1 est impulsionnelle (brèves impulsions de courant dans la diode) et donc que la chute de tension à l’instant de l’impulsion est très supérieure à ce que donnerait la valeur moyenne.
On a donc une chute de tension très grande par rapport à un simple diviseur à résistances R1 et R2.
Je ne vois pas comment on pourrait prévoir par le calcul, le temps d’ouverture de la diode, la valeur de l’impulsion de courant… 
Bonsoir Transistorix,
Nous sommes bien d’accord !
Je précise que c’est juste pour le « fun », quoique…
J’ai transformé le schéma avec Thévenin, j’ai pris le développement en série de Fourier d’un cosinus
qui vaut 0 s’il est négatif, j’ai écrit la petite équation différentielle pour la tension instantanée aux bornes de C
et je l’ai résolue mais… ça coince justement sur la valeur max.
Alors j’ai fait ce petit PSpice qui me donne un résultat Vmax aux bornes de C qui me laisse bien perplexe.
Je serais curieux de savoir comment procède PSpice à l’intérieur dedans de lui-même !
Le but réel étant l’étude du comportement de MF2 et de la détection AM qui le suit.

Voui Jean-Claude !
Je suis toujours émerveillé de constater qu’un schéma ma foi fort simple se révèle aussi ardu au calcul !
Mais ce que fait PSpice, je devrais pouvoir le faire à la main quand même, non ?

Je pense qu’il faut avoir les courbes caractéristiques de la diode et tracer les droites de charge statique et dynamique. Je vais aller consulter les Terman et autres Sturley ou Happell & Hesselberth…
Dommage que dans PSPICE il n’y ait pas un modèle de diode « idéale » (go/no go) à but purement pédagogique !
Je reste très pessimiste pour le calcul.
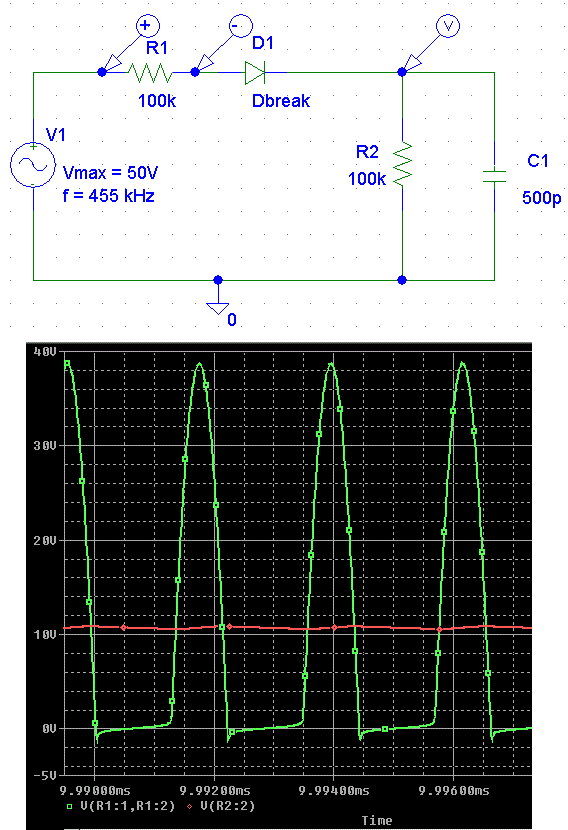
Si on prend un cas simple ou R1 = R2 et V max = 50V (doc joint), on pourrait s’attendre à ce la tension de sortie soit 25 V, ce qui est faux.
La vraie valeur de la tension de sortie (11 V) sortira de l’équation :
Même courant moyen dans R1 et R2 → VR1moy = VR2 moy (puisque R1 = R2)
D’après la simulation jointe, on voit que VR1moy = VR2moy = 11 V et VR1max = 39 V.
Il faudrait donc arriver à démonter que le maxi de la tension R1 (qui est la chute de tension) est égal à 39 V…
Reste plus qu’à résoudre le système :
VR1moy = VR2moy
VR1max + VR2moy = Vmax = 50V
Bon courage 
Bonjour,
Si 2*tc est le temps d’ouverture du circuit (temps pendant lequel la diode conduit), on peut calculer la charge transférée au condensateur pendant ce temps en simplifiant, en considérant que la tension d’alimentation est constante pendant toute la durée d’ouverture et égale à V0 tension crête du générateur. Le condensateur se charge à travers R1, on néglige aussi l’effet de R2 (nettement plus grande que R1) pendant ce temps là :
Qcharge = intégrale de -tc à+ tc de ( (V0cos(Wt) - Vs)/R1)*dt ) c’est à dire :
Qcharge = 2*[V0sin(Wtc)/W - Vs*tc]/R1
En supposant que le temps d’ouverture est faible, on peut probablement assimiler le sinus à l’angle et simplifier en :
Qcharge = 2*(V0-Vs)tc/R1 ce qui revient à considérer que le courant pendant la pointe de l’ouverture de durée 2tc est constant et égal à (V0-Vs)/R1 et c’était pas la peine de s’embêter à intégrer.
Pendant la décharge, la diode ne conduit pas et le condensateur se décharge dans R2 uniquement :
Qdécharge = CVs(1-exp(-T/R2C))
A l’équilibre (temps long) les 2 charges doivent être égales, ce qui donne une relation entre Vs et tc :
tc = ((R1C)/2)(Vs/(V0-Vs))(1-exp(-T/R2C))
L’exposant dans l’exponentielle vaut environ -0.2 et on peut développer l’exponentielle :
2*tc = (R1/R2) * (Vs/(V0-Vs)) T
Je n’arrive pas à trouver, malheureusement, une deuxième équation indépendante pour déterminer les 2 inconnues (tc et Vs).
Tout ce qu’on peut faire est de calculer tc en utilisant le résultat de la simulation pour Vs (27 V).
En prenant plutôt Vs = 25 V, VS/(V0-Vs) =1 et
2*tc = (85/500) * T
C’est à dire que le temps d’ouverture 2*tc vaut 17% de la période. Il faudrait dans la simulation tracer le courant ou la tension aux bornes de R1 comme l’a fait J.C. Jardine mais avec les valeurs originales de 85K, 500K et 100pF et vérifier si la largeur de la pointe du courant est de l’ordre de 17% de la période.
edit : J’ai remodifié le pourcentage de la période, 2*tc vaut bien 17% de la période dans mon calcul.
Voila la simulation avec les valeurs d’origine (doc joint).
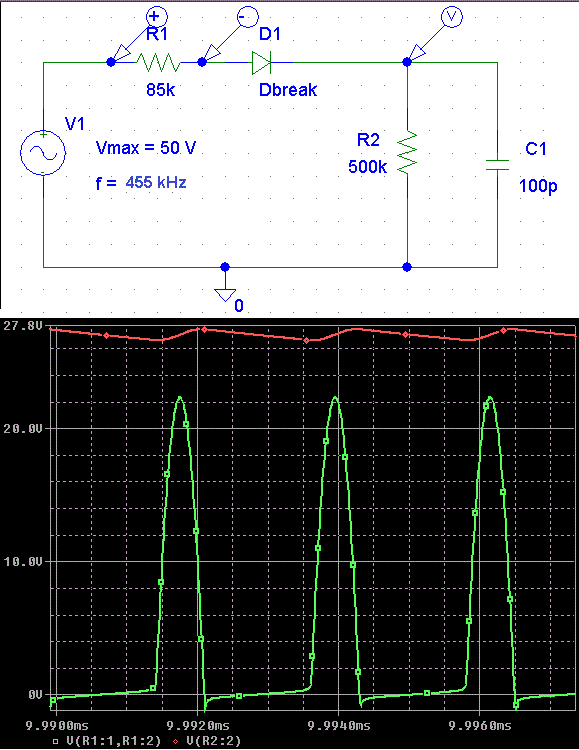
La largeur de l’angle d’ouverture fait de l’ordre de 27% de la période dans votre simulation.
Je me suis embrouillé dans les facteurs 2 et je viens de corriger encore le calcul de mon pourcentage qui fait bien 17% ce qui est quand même loin de la réalité de vos 27%. Je ne sais pas si ce sont mes approximations qui sont trop brutales ou si c’est le calcul lui même qui est incorect.
Bonsoir Jean-Claude et JeffM, bonsoir à tous,
Merci de vos réponses.
Pas simple effectivement.
Ne pourrait-on pas dire que la tension max aux bornes de C est le point de la sinusoïde où :
la tension de départ du petit cycle de charge est égale à celle de la fin du petit cycle de décharge ?
Comme ces points répondent à l’équation du cos et aux équations de charge et décharge, ça devrait donner un système mélangeant du cos et de l’exponentielle, système peut-être résoluble ?
Bon, comment fait le moteur de PSpice pour trouver ce max ?
JeffM,
Avez-vous repéré que j’ai finalement trouvé l’expression algébrique de k critique ?
http://www.forum.retrotechnique.org/viewtopic.php?f=1&t=243389
Il me faudrait une grande bande de papier pour l’écrire…

Si j’utilise bien 27 v et non 25 V que j’avais introduit pour qu’un des facteurs de la formule vale 1, j’arrive à la valeur
2tc/T= (R1/R2)(Vs/(V0-Vs) = (85/500)*(27/(50-27)) = 19.96%, pratiquement 20%.
Je me rapproche un peu des 27% mais je suis encore loin.
à J.P. Waymel
J’ai bien remarqué mais je n’ai pas compris pourquoi vous avez 3 solutions à votre équation du 3ième degré (dont une double qui donne un point d’inflexion dans la courbe de réponse), au couplage critique il me semble qu’il ne devrait y avoir qu’une seule solution.
Bonsoir,
Peut être en supposant que les petites variations de la tension autour des 27 Volts peuvent être négligées et, en se limitant au régime établi on doit pouvoir écrire l’égalité des quantités d’électricité soit :
Valeur moyenne du courant de charge lorsque la diode est saturée par une tension V1*R2/(R1+R2) > Um
Là il faut faire une peu de trigo pour calculer la surface d’une sinusoïde qui dépasse une certaine valeur.
Puis la quantité d’électricité que cela peut créer à travers R1//R2.
Cela ne me parait pas insurmontable…
Tx
Je pense que c’est exactement ce que je fais sauf que je calcule les charges (qui se conservent) et non les courants (qui ne se conservent pas).
Je pense que l’approximation la plus grossière que je fais est d’assimiler le sinus à l’angle. En effet, si l’angle d’ouverture est de l’ordre du quart de la période (2Pi)/4, ça fait un angle de l’ordre de Pi/2 dont le sinus est 1 et approximer 1 à Pi/2 (1.57), c’est pas terrible.
En réécrivant l’équation sans faire cette approximation, je trouve l’équation suivante dans laquelle je suis passé en angle plutôt qu’en temps (Theta= Wt) :
sin(Thetac)-(Vs/V0)*Thetac = (Vs/V0) * (R1/R2) * Pi soit en valeurs numériques (Vs=27, V0=50, R1/R2=0.17) :
sin(Thetac) - 0.54*Thetac = 0.2884
Il ne reste plus qu’à résoudre numériquement ou graphiquement cette équation.
Voila la solution graphique :
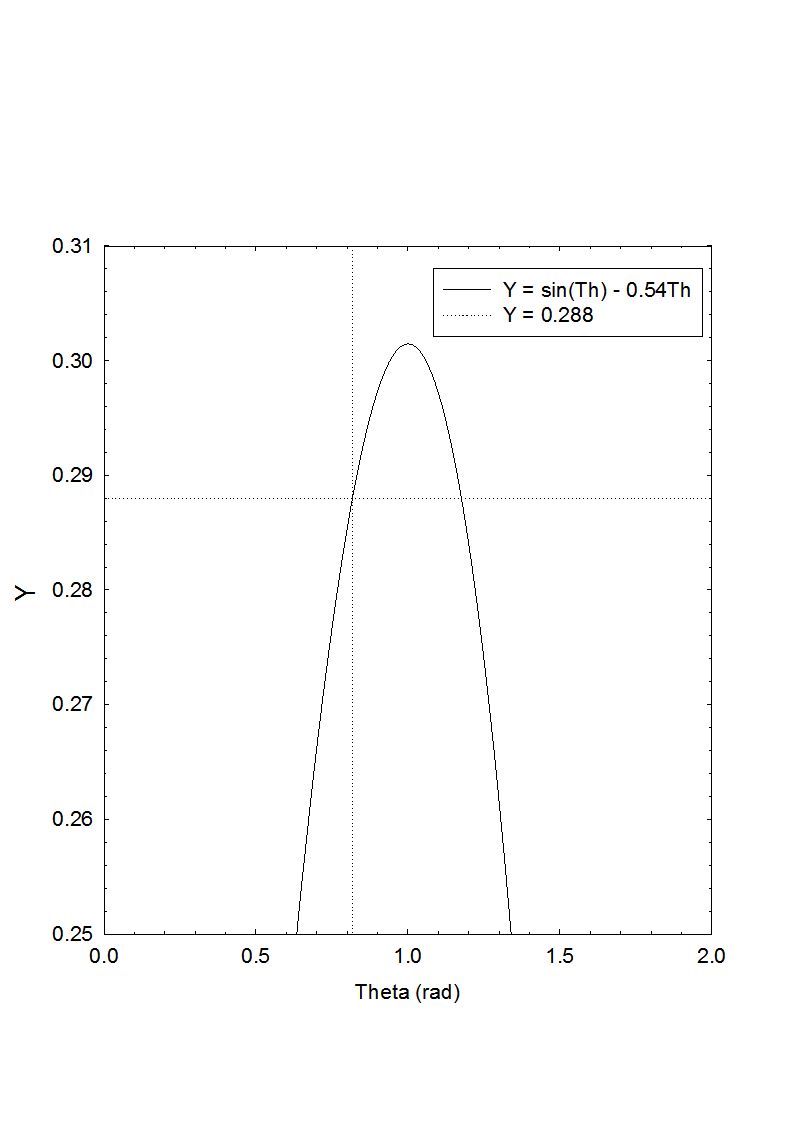
Il y a 2 solutions, la première se trouve à Thetac = 0.82 c’est à dire 2Thetac = 1.64 rad
(2Thetac)/2Pi) = 0.261
L’angle d’ouverture vaut donc bien 26% de la période, ouf.
Il faudrait justifier que c’est bien cette solution qu’il faut prendre et pas la deuxième.
Maintenant il faudrait trouver la seconde équation qui permettrait de résoudre complétement le problème numériquement ou graphiquement, pour le moment je sèche.
Pour JeffM,
Maxis/mini du gain du transfo MF : je te réponds sur le fil en question afin de ne pas trop brouiller celui-ci.
Puis j’étudierai ici bien sûr vos réponses à tous sur le sujet en cours.
C’est intéressant. Merci beaucoup.
Bonjour,
Pour illustrer, le problème se ramène a calculer la surface de la partie jaune lorsque la barre horizontale se déplace.
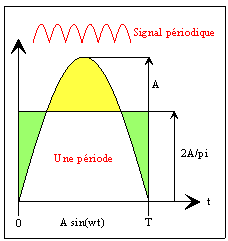
En déduire la valeur du courant moyen, et ensuite écrire que la somme des courants dans le condensateur sur une période est nulle.
Ce qui aboutira finalement a une équation impossible a résoudre directement.
Donc la simulation n’est peut être pas une si mauvaise idée.
Tx
Bonjour,
vias.org/eltransformers/lee_ … 04_03.html
En //, je vais essayer de suivre la piste de la biblio…
Bonjour,
Le cas du redressement dans le cadre d’une alimentation est un peu différent car la résistance de source (résistance du transfo) est beaucoup plus faible que les 85K de R1 de ton problème et la nature non linéaire de la diode joue considérablement, sa résistance n’étant jamais négligeable devant celle de la source d’où un calcul extrêmement compliqué. Dans ton cas, compte tenu des 85K, la diode peut être assimilée à une diode parfaite (interrupteur ouvert ou fermé). Spice utilise certainement l’équation classique de la diode mais les résultats ne peuvent pas être très différent de ceux obtenus avec une diode parfaite, la résistance de la diode (non parfaite) lorsqu’elle conduit étant négligeable devant 85K quelque soit le courant qui la traverse.
Je suis maintenant capable de retrouver l’équation qui relie l’angle d’ouverture et la tension de sortie de trois façons différentes (conservation de la charge, conservation de l’énergie, résolution d’équat diff décrivant charge et décharge de C) la plus simple étant l’utilisation de la conservation de l’énergie, mais, malgré mes efforts, je retombe toujours désespérément sur cette même et unique équation :
(Vs/V0) = sin(?c)/(?c + ?*(R1/R2))
où Vs est la tension de sortie, V0 la tension crête du générateur, ?c, le demi angle d’ouverture (?tc). En reprenant le résultat mesuré sur la dernière simulation de J.C. Jardine, 2(?c) vaut approximativement 27% de 2*? soit ?c = 0.85 radians et Vs/V0 vaut 0.543 soit Vs = 0.543*50 = 27.1 V ce qui montre que cette équation est tout à fait raisonnable. Reste à en trouver une autre.
Bonjour à tous,
OK JeffM !
Vois le lien mentionné juste avant.
Le graphe donne le rapport « tension CC en sortie /tension max en entrée » en fonction du rapport R1/R2 soit ici
85 /500 = 0,17 (en supposant nulle la R de la diode quand elle est conductrice mais de toute façon elle est faible devant R1), de la fréquence, de C et de R2.
J’ai remonté la piste jusqu’à D.L. Waidelich. Mais il y a un copyright IEEE : 31 US$ + frais !
J’ai une idée pour les équations mais le pb consistera ensuite effectivement à trouver les angles d’ouverture et de fermeture du courant diode.
Le temps manque. Du moins, j’ai des tâches domestiques (travaux) à finir, avec des contraintes de dates…  Donc à suivre dans quelque temps !
Donc à suivre dans quelque temps ! 