Bonjour à tous.
Puis-je apporter mon grain de sel ?
Quel est le modèle de diode utilisé pour ce schéma ?
Il me semble qu’il existe deux modèles de diodes réelles, soit sous forme de tableau, soit sous forme de courbes.
Dans les deux cas il apparait, soit une capacité, soit un temps de recouvrement des charges stockées dans la jonction. Ce qui veut dire qu’il existe un courant inverse peut être non négligeable - à cette fréquence - qui ne peut pas être pris en compte dans un modèle de diode parfaite.
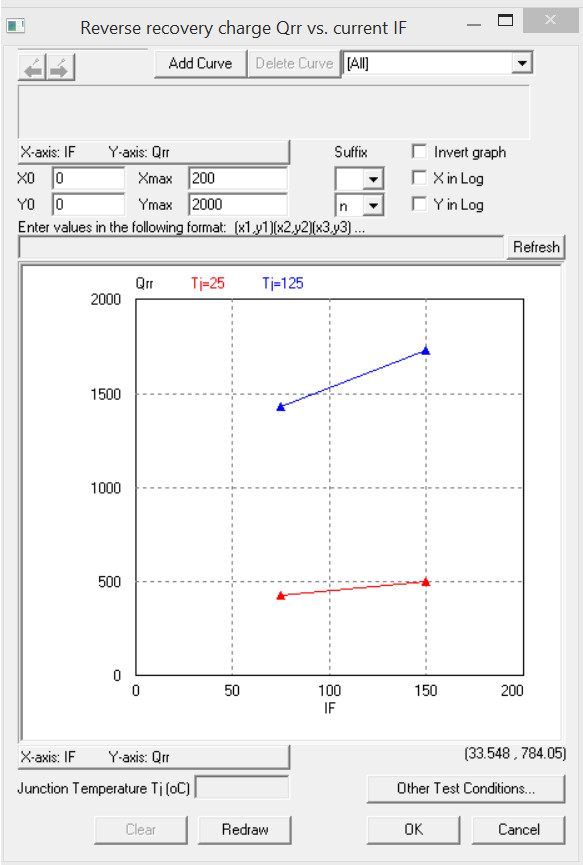
Ici, un fichier concernant une diode zener où on distingue la valeur Cjo=78p :

Ainsi les calculs ‹ à la main › sont relativement illusoires sans la connaissance de cette donnée.
… et deviennent inextricables en la connaissant !
Il me semble me souvenir de calculs matriciels appliqués à des réseaux, déterminant de proche en proche la valeur de la grandeur à déterminer jusqu’à ce que la variation à chaque étape du calcul devienne inférieure à une valeur fixée… le tout codé dans un paquet de 15 cm de cartes perforées !
Bonsoir à tous,
jfcrois, toutes les interventions sont utiles et appréciables !
PSpice me donne une idée de l’ordre de grandeur des tensions et courants ainsi que leurs allures.
Ici, si mes souvenirs sont exacts, DBREAK est un modèle tout nu, avec juste une tension de seuil.
Sinon, dans le cas qui m’occupe, il s’agit d’une diode à vide qui pourra être assimilée à une simple résistance constante ou à une résistance constante plus une chute de tension constante. Je verrai ensuite à utiliser sa vraie courbe de réponse I(V), surtout pour les petits signaux…
En tout cas, PSpice indique une tension CC de sortie en parfait accord avec l’étude faite par D. L. Waidelich (1941) et les courbes tracées ensuite par Schade (voir mon lien un peu plus haut).
O. H. Schade : Analysis of Rectifier Operation, Proc. I.R.E., 31, 341 (July, 1943).
Pour revenir à PSPICE, voici comment est traitée une diode :
http://www.ecircuitcenter.com/SpiceTopics/Non-Linear%20Analysis/Non-Linear%20Analysis.htm,
un processus effectivement itératif.
Bon, je vais me remettre à la recherche des équations…
Bonsoir,
Vous avez raison, le calcul du circuit réel à la main est illusoire et seul un simulateur avec un modèle sérieux de la diode pourra le faire, ici il s’agit seulement d’essayer de décrire dans un but pédagogique le comportement du circuit et pour cela un modèle de diode idéal suffit largement, c’est déjà assez difficile comme çà.
Il semble que DBREAK soit un modèle avec l’équation exponentielle classique de la diode avec un courant de saturation inverse de 1E-14 A, une résistance série de 0.1 Ohms et une capacité de jonction de 0.1 pF. Les éléments parasites (Rs et Cj) ne devraient pas trop gêner à 455 kHz devant R1.
Selon D. L. Waidelich (voir pièces jointes) :
i_L = i_? à ?=? avec ?=?t
A ?, la diode commence à conduire.
q_? est la charge de C à ?=?.
Jusqu’à ? où elle se bloque.
Yapuka déjà résoudre l’équation différentielle en i_C par exemple qui doit avoir une allure en
a x di_C/dt + b x i_C + c x sin(?t) = d.
Avec la condition i_L = i_? à ?=? avec ?=?t.
Chaud !

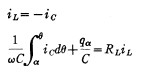

OK Jeff pour DBREAK ! Effectivement, ça devrait le faire… Une tension de seuil peut-être ?
J’ai déjà exploré plus ou moins cette voie en simplifiant un peu (pendant la conduction, je remplace V0cosWt par V0 ce qui revient à assimiler la pointe sinusoidale du courant à un rectangle.)
En écrivant aussi l’équation dif pendant le blocage de la diode, on obtient 2 équations donnant Vmax et Vmin de l’oscillation autour de Vs moyen en fonction de l’angle d’ouverture mais, après simplification, je ne récupère que toujours la même équation maudite plus ou moins simplifiée.
J’espère que mes gribouillis sont lisibles
demo.ovh.eu/download/3b026e7ba96 … sement.pdf
J’arrive à une équa diff’ genre :
(R_L // R_R) di_C / d? + i_C / (?C) - E_m x cos? x R_L / (R_L + R_R) = 0
mais pas sûr car V et q_? ont disparu. Ou alors ils vont revenir avec les conditions initiales ?
On a (je pense) : q_? / C = R_L x i_? ?
Oui les gribouillis sont lisibles !
Bon, ça avance… J’ai le coefficient de sin? pour i_c !
A suivre !
<edit 04 déc 2014 00:54>
i_C, i_L et i_R entièrement calculés pour la phase de charge : de jolies expressions…
A suivre : idem pour la phase de décharge.
Bonsoir,
Expressions littérales exactes des courants pendant les phases de charge et de décharge : OK, fait.
Yapuka égaler début de charge et fin de décharge.
Ca va donner des équations en e^t x sin(t) et e^t x cos(t) qui ne pourront être résolues que graphiquement, comme on s’y attendait.

J’ai suivi la superbe méthode de D.L. Waidelich.
On va pouvoir aussi calculer la ronflette… car le modèle est identique pour une alim’ simple ou une alim’ double alternance (dans les équations, il suffira de mettre n=1 pour simple alternance ou n=2 pour double alternance).
@suivre.
J’ai refait les calculs un peu plus complétement, sans l’approximation qui consistait à prendre l’impulsion de courant rectangulaire.J’obtiens ainsi 2 équations sans approximations (sauf l’idéalité de la diode) qui donnent Vmax et Vmin (et Vs si on suppose que Vs est la demi-somme de ces quantités) en fonction de l’angle d’ouverture, mais comment déterminer cet angle ?
La conservation de l’énergie donne, en fait, le même résultat simplifié car je suppose que Vs est constant sur toute la période, C’est à dire que C est suffisamment élevé (R2CW>>1) pour qu’il n’y ait pas de ronflement. C’est le domaine de la figure 50 de ton lien précédent où les courbes sont toutes horizontales et donc indépendantes de R2CW.
Je ne sais toujours pas comment déterminer l’angle d’ouverture indépendamment de Vs.
Voir la pièce attachée ici :
demo.ovh.eu/download/c67cd04c103 … ideale.pdf
Bonjour JeffM, bonjour à tous,
Dès que j’ai fini mes petits calculs, j’en ferai ici un résumé : méthode et résultats.
Amicalement.
Bonsoir,
Ceci ne ressemblerait pas un petit peu à ce que vous cherchez à calculer ?
Numériser0001.pdf (62.2 KB)
Tx
Bonsoir,
C’est un problème voisin mais beaucoup plus simple. Ici, il s’agit simplement de calculer la valeur moyenne (et la valeur RMS ) de la tension à la sortie d’un circuit à thyristor dont on se donne à priori l’angle à partir duquel le thyristor conduit. Cet angle est fixé par le circuit de gâchette qui n’est pas représenté. Le calcul est simple, il suffit d’intégrer entre alpha et Pi la fonction E*sin(Theta) et diviser le résultat par 2Pi (cas du premier dessin mono-alternance).
En ce qui concerne le ronflement, la valeur à l’angle thetac=0.85 (voir figure 2 de ma dernière pièce attachée) donne (Vmax-Vmin)/V0=0.0174, soit une valeur crête-crête de 0.87 V autour de la valeur moyenne de Vs de 27.13 V.
Bonsoir,
Après beaucoup de tâtonnements trigonométriques, voici les jolies égalités qui permettent de déterminer l’angle de début de conduction ? et l’angle de début de blocage ? de la diode (ou des diodes) :

J’ai suivi la méthode de D.L. Waidelich (1941) mais j’ai eu beaucoup de difficultés à la fin pour simplifier une expression et arriver à la formule n° II (D.L. Waidelich ne détaille pas trop ses calculs).
Bon, une fois que l’on a trouvé, c’est évident, comme d’hab’.
Yapuka résoudre ce système de 2 équations à 2 inconnues, système éminemment non linéaire !
Evidemment, la résolution sera graphique.
R_R(ectifier), c’est ma R1 + la résistance interne de la diode passante.
R_L(oad), c’est ma R2.
@suivre…
Bonjour,
Beau travail,
Finalement cela ne fait que 2 équations a 2 inconnues !
Tx
Bonjour à tous,
Voui, Transistorix, merci !
C’est surtout Waidelich qu’il faudrait féliciter (dans l’au-delà ?).
L’intérêt du truc, c’est que c’est valable pour la détection MA dont la CAG comme pour le redressement simple ou double alternance.
La suite : résolution graphique pour avoir les valeurs des 2 angles, calcul de la tension moyenne de sortie, de l’ondulation, etc.
Le tout ayant donné lieu aux abaques encore utilisées de nos jours (voir la référence plus haut dans ce fil de discussion).
Pour l’instant, je m’intéresse à la détection MA qui fait suite à MF2.
Dans le cadre général du re-calcul de chaque élément d’un poste.
J’avais besoin de connaître l’étagement des différents gains, d’où l’étage tube + MF2 et maintenant la détection MA.

Bonjour,
Beau travail. La résolution numérique s’avère délicate. Je crois que dans un premier temps, on peut commencer à faire V=0 pour revenir au détecteur idéal du problème d’origine, et même comme çà, c’est pas trop simple.
Entre temps je me suis procuré l’article de Waidelich et, comme d’habitude, je comprends mal ce style de publications. Dès la figure 2 j’ai du mal avec le courant qui traverse la diode (iR). Pour quelle raison y a t’il une discontinuité avec saut du courant au début de la conduction (angle alpha) ? Lorsque la diode commence à conduire, la tension à gauche de la diode tension du générateur est tout juste égale à celle à la droite de la diode (tension de sortie) et le courant qui était nul avant que la diode ne conduise commence tout juste à monter quand elle commence à conduire et devrait donc partir de zéro. C’est bien ce qu’on voit sur la simulation de J.C. Jardine, le courant part de zéro et y revient à un microtransitoire négatif près. De même l’angle béta est défini dans le texte comme l’angle pour lequel le courant s’annule. C’est probablement vrai pour un détecteur à vapeur de mercure, un fois ionisé, le tube conduit jusqu’à l’annulation du courant mais pas pour un tube à vide, dans ce cas, le courant devrait s’annuler lorsque la tension à gauche est juste égale à la tension à droite, c’est à dire symétriquement à l’angle alpha par rapport au sommet de la demi sinusoide du générateur. La figure 2 correspond probablement à un tube à vapeur de mercure mais ça ne m’explique pas le comportement à l’angle alpha. Je suppose que c’est la source V sensée simuler la chute de tension indépendante du courant aux bornes de la diode qui est responsable de cet effet, mais je ne le comprends pas bien. V n’est pas une vraie source de tension, juste une chute de tension.
Bonsoir,
A JeffM,
Le seul mérite revient à D.L. Waidelich (1941).
Je me suis simplement efforcé à retrouver ses résultats de calcul. Juste pour le fun.
L’ennui, c’est qu’il y a un copyright sur son article sinon je l’aurais publié in extenso pour faciliter les discussions.
Pour trouver les angles, il fait un changement de variable astucieux : ? = ? - ?.
On obtient alors les 2 équations suivantes :
A1 sin(?) + B1 cos(?) = C1
A2 sin(?) + B2 sin(?) = C2
faciles à résoudre.
Cela donne donc une valeur pour sin(?) et un angle ?1 ainsi qu’une valeur pour cos(?) et un angle ?2.
On trace ?1 et ?2 en fonction de ?.
Comme ?1 = ?2, l’intersection des 2 courbes donne la valeur de ? et de ? donc de ?.
Voici la figure 2 qui correspond à vos commentaires :
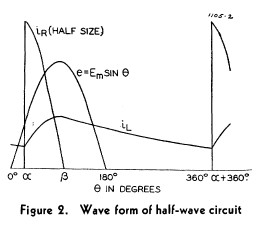
Oui, moi aussi je trouve curieux ce « front » brutal de montée de i_R.
Ca ressemble à un courant de départ « à travers » un condensateur déchargé…
i_R part bien de 0 en ?.
Pour mieux comprendre le truc, Il faudrait tracer sur la même figure la tension de sortie.
Quant à V, c’est effectivement pour simuler la chute de tension d’un redresseur à vapeur de mercure.
Il y a eu une discussion sur cet article avec entre autres Terman.
Je vais aller voir si cela apporte des éclaircissements.
Il y a aussi les autres articles cités dans la bibliographie mais sans doute aussi des copyright…
Il semble bien que le front vertical de i_R corresponde au cas où R_R est très faible.
Voici ce que disait Reuben Lee à Waidelich (extrait) :

 Doctsf (Modèles & Marques)
Doctsf (Modèles & Marques) Annonces
Annonces